算法刷题

字符串搜索

主串A: a, b, c, d, e, f, g

模式串B: c, d, e

判断B是否在A中, 存在返回在A中的下标, 不存在返回-1

再如: A: ABCABCAABCABCD; B: ABCABCD; 返回值7.

BF: 暴力破解

复杂度O( (n-m)*m )

 1//BF:暴力破解
 2    int BF(String A, String B){
 3        int aLength = A.length();
 4        int bLength = B.length();
 5        //这里aLength - bLength稍微优化了一下
 6        for (int i = 0; i <= aLength - bLength; i++) {
 7            int j;
 8            for (j = 0; j < bLength; j++) {
 9                if (A.charAt(i+j) != B.charAt(j)){
10                    break;
11                }
12            }
13            //需要判断上面的子循环什么时候将B完整遍历了一遍
14            //当j=B.length时, 刚好执行了最后一次j++
15            if(j == B.length()){
16                return i;
17            }
18        }
19        return -1;
20    }

RK算法: hash算法

基于BF进行优化, 将A中的字符串按照顺序截取B字符串的长度: abc, bcd, cde, def, efg. 进行hash运算然后与B的hash值进行比较. 时间复杂度: O(m*n), hash算法参与字符串位数, 主串长度相关.

优化: hash算法: 按26进制取和, abc=1+2+3=6, 进行量化. 每个子串的hash值是前一个子串的hash值-前串最小下标对应字母的值+本串最大下标字母对应的值.

此时间复杂度为O(n), 只与主串长度相关, 但hash冲突极端情况下退化为BF

 1//RK:hash算法
 2    static int RK(String A, String B){
 3        int aLength = A.length();
 4        int bLength = B.length();
 5        int bCode = B.hashCode();
 6        for (int i = 0; i <= aLength - bLength; i++) {
 7            String aSub = A.substring(i, i + bLength);
 8            if(aSub.hashCode() == bCode){
 9                //防止hash碰撞
10                int j;
11                for (j = 0; j < bLength; j++) {
12                    if (aSub.charAt(j) != B.charAt(j)){
13                        return -1;
14                    }
15                }
16                if (j == bLength){
17                    return i;
18                }
19            }
20        }
21        return -1;
22    }
23
24    //RK: hash算法 优化hash
25    static int hashCode(String string){
26        int hashCode = 0;
27        //初始化字母表
28        HashMap<Character, Integer> map = new HashMap<>();
29        int base = (int)'A'-1;
30        for (char c='A'; c<='Z'; c++){
31            map.put(c, (int)c-base);
32        }
33        for (char c='a'; c<='z'; c++){
34            map.put(c, (int)c-base);
35        }
36
37        for (int i = 0; i < string.length(); i++) {
38            hashCode += map.get(string.charAt(i));
39        }
40        return hashCode;
41    }

BM算法

1.坏字符规则: 从右往左匹配, 找到A中第一个不匹配的字符(坏字符), 将B串右移, 直到出现与A串坏字符对齐的字符, 再从右往左寻找坏字符. 如果B串中没有该坏字符, 则直接移到该坏字符的下一位即可.

例如A串:ABCABCAABCABCD; B串ABCDBC. A串前6个为ABCABC, 初始从右往左匹配, 这时B串的C与A串该位置的C对应, 继续匹配B, 然后B串中的D与A串中的对应位置A不匹配, 出现换字符.

1ABCABCAABCABCD
2ABCDBC

于是右移B串, 第一个与A坏字符对应的B串位置就是第一个字母, 现在变成了

1ABCABCAABCABCD
2   ABCDBC

B串往右移动了两格. 又开始从右往左寻找坏字符, 这时第一个B与C就冲突了, 于是又开始右移, 对齐这个坏字符:

1ABCABCAABCABCD
2    ABCDBC

B串往右移动一格后坏字符对齐, 又开始从右往左寻找坏字符, A与D出现冲突, 右移:

1ABCABCAABCABCD
2       ABCDBC

B串右移三格. 这一次再移动一格就到头了, 不行.

坏字符规则是从右往左比较的, 并且这个移动规则保证了跳过多余的比较同时又不会遗留.

2.好后缀规则: 从右往左匹配, 找到坏字符(坏字符后面的串是匹配的, 是好串), 往左寻找B中是否还有该好后缀, 如果有, 将B右移到该位置与A好后缀进行对齐. 重复该规则. 如果B串往右没有该好后缀, 则右移到好后缀的往右错一位的位置, 重复该规则. 避免B串的前缀与好后缀的后缀匹配

还是以上面为例:

1ABCABCAABCABCD
2ABCDBC

这时好串是BC, 往前寻找发现还有这个好后缀, 于是进行对齐:

1ABCABCAABCABCD
2   ABCDBC

这时坏字符是第一个, 没有好串, 只有先对齐了:

1ABCABCAABCABCD
2    ABCDBC

有好串了, 继续

1ABCABCAABCABCD
2       ABCDBC

在移动就超过长度了, 于是没有匹配的.

再举有匹配的一例:

 1ABCABCAABCABCD
 2ABCABCD
 3开始位置0; 坏字符下标:6; 需要移位:3; 
 4
 5ABCABCAABCABCD
 6   ABCABCD
 7开始位置3; 坏字符下标:6; 需要移位:1; 
 8
 9ABCABCAABCABCD
10    ABCABCD
11开始位置4; 坏字符下标:6; 需要移位:3
12
13ABCABCAABCABCD
14       ABCABCD
15开始位置7; 无坏字符.

两种规则综合使用, 哪种移动的位数多使用哪种

时间复杂度: O(n/m), 最坏O(m*n)

 1//BM
 2    static int BM(String A, String B){
 3        int aLength = A.length();
 4        int bLength = B.length();
 5        //每次操作结束后A串对齐B串的标志位
 6        int index = 0;
 7        while (true) {
 8            for (int j = bLength-1; j > 0; j--) {
 9                //出现坏字符
10                if (A.charAt(index + j) != B.charAt(j)){
11                    Boolean ifHaveBad = false;
12                    for (int i = j; i > 0; i--) {
13                        //B串中有坏字符
14                        if (A.charAt(index + j) == B.charAt(i)){
15                            ifHaveBad = true;
16                            index += j-i;
17                            break;
18                        }
19                    }
20
21                    if (!ifHaveBad){
22                        //B串中没有坏字符, 应移位到坏字符下一位
23                        index += j;
24                    }
25
26                    //如果已经不能再移位了, 说明没有匹配的.
27                    if (aLength - index < bLength) return -1;
28
29                    //移位, 进行下一次规则循环比较.
30                    break;
31                }
32                //在B串一次循环中没有一次进入if分支, 说明全部匹配
33                return index;
34            }
35        }
36    }

KMP算法

前缀: 字符串A=B+S, S非空, 那么B就是A的前缀

后缀: 字符串A=S+B, S非空, 那么B是A的后缀

PMT值: 前缀集合和后缀集合的交集中, 最长元素的长度

部分匹配表: PMT值集合, 字符串的所有前缀的PMT值

perfix数组: 每一个下标位置对应一个PMT值, 组成的数组

next数组: perfix向右移一个下标位置, 组成next数组

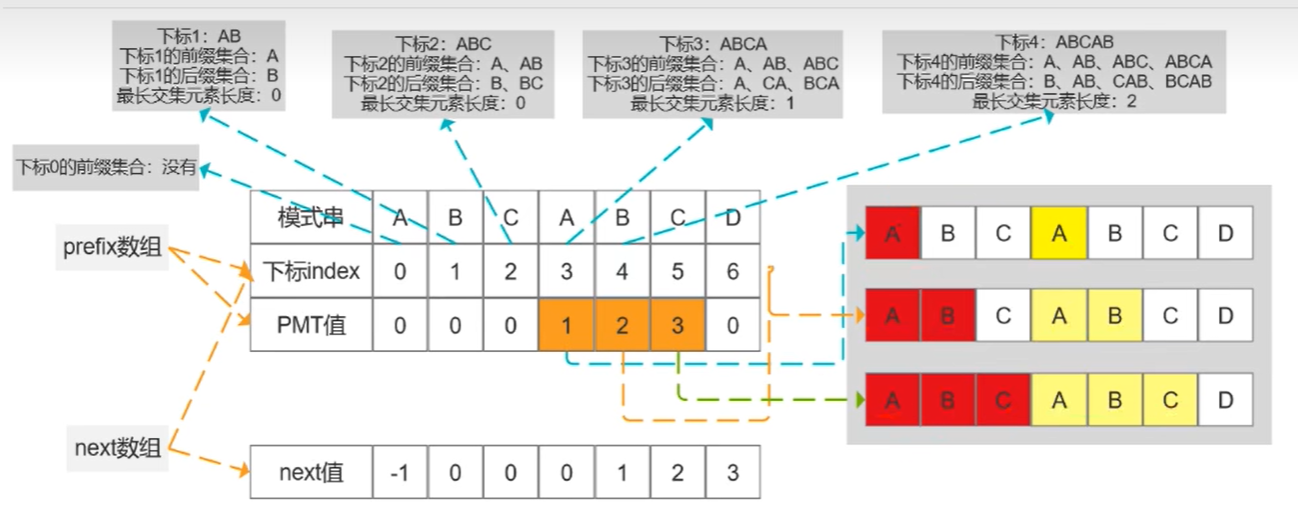
这个PMT值就是我们每次找到坏字符后, pattern字符串需要移动的距离.

求next数组:

 1//KMP: next数组生成
 2    static void getNext(char[] pattern, int[]next){
 3        //next数组其余位置默认是0.
 4        next[0] = -1;
 5        int i = 0, j = -1;
 6
 7        while (i < pattern.length){
 8            //每当j=-1时, 就是说明当前子串已经找完了.
 9            if(j == -1){
10                i++;
11                j++;
12            }else if(pattern[i] == pattern[j]){
13                i++;
14                j++;
15                //这时i位置上的值赋值的是i-1位置上的KMP值, 错位了.
16                next[i] = j;
17            }else {
18                //当字母不匹配后回到这里, j慢慢缩小直到-1.
19                j = next[j];
20            }
21        }
22    }

以ABCABCD串解释如何求出next数组.

1.默认情况下i=0, j=-1, 这时刚好寻找下标为0子串的KMP值, 这是肯定为0的, 所以我们进行i++,j++.

1ABCABCD
2ABCABCD

2.现在变成了i=1, j=0; 由于此时B != A, 说明子串AB的KMP值为0, 于是将j赋值为-1, 这样i就会++. 表明这个位置没有匹配的, 仍需要移动

1ABCABCD
2 ABCABCD

3.现在i=1, j=-1, 又变成i=2, j=0, C!=A, 第一个仍然不匹配, 继续

1ABCABCD
2  ABCABCD

4.现在i=3, j=0, 匹配了, 将next[4] = 1, i++, j++后继续匹配, next[5] = 2, i++, j++后继续匹配, next[6] = 3, 当i=6, j=3时, 不匹配了, 又回到j=0了, 然后j=-1, 最后i = 7 = pattern的长度了.

1ABCABCD
2   ABCABCD

最后一个问题, j = next[j];是否一定会让j变成-1, 有没有例外情况? 我们举例来看看:

1如果串是: ABCABCDABCDA
2
3ABCABCDABCDA
4       ABCABCDABCDA
5这时i=10 j=3时不匹配, 那么j=next[3]=0

初步估计这个next数组是越来越大的, 因为子串的长度在不断增大, KMP值越来越大, 所以它总会收敛于-1的.

算法本体:

 1//KMP
 2    static int search(char[] str, char[] pattern, int[] next){
 3        int i = 0;
 4        int j = 0;
 5
 6        while (i < str.length && j < pattern.length){
 7            if (j == -1 || str[i] == pattern[j]){
 8                i++;
 9                j++;
10            }else {
11                //不匹配了 , 就往后移动.
12                //所以下标0的-1也是移动的手段,
13                j = next[j];
14            }
15        }
16
17        //如果j最后一直到了最后都和i匹配, 说明找到了.
18        if (j == pattern.length){
19            return i - j;
20        }else {
21            return -1;
22        }
23    }

测试:

 1public static void main(String[] args) {
 2        String A = "ABCABCAABCABCD";
 3        String B = "ABCABCD";
 4        System.out.println(BF(A, B));
 5        System.out.println(RK(A, B));
 6        //System.out.println(hashCode(B));
 7        System.out.println(BM(A,B));
 8
 9        int[] next = new int[B.length()];
10        getNext(B.toCharArray(), next);
11        int i = search(A.toCharArray(), B.toCharArray(), next);
12        System.out.println(Arrays.toString(next));
13        System.out.println(i);
14        System.out.println(A.indexOf(B));
15    }

打家劫舍

动态规划三要素:

最优子结构: 每一个问题的最优解都包含子问题的最优解(n的最优依赖的是n-1的最优)
递推公式(状态转移方程): 找问题的规律, 解和前面解的关系
重叠子问题

初始问题

问题: 小偷偷钱, 不能偷相邻的房间. 给定一个代表每个房屋存放金额的非负整数数组, 计算你不触动警报装置的情况下, 一夜能偷窃到的最高金额

输入: [1,2,3,1] 输出:4

输入:[2,7,9,3,1] 输出12

 1public class Rob {
 2
 3    public static void main(String[] args) {
 4        int[] num = new int[]{100, 2, 1, 100};
 5        int index = num.length -1;
 6        System.out.println(maxMoney(num, index));
 7        System.out.println(maxMoney2(num));
 8    }
 9
10
11    static int maxMoney(int[] num, int index){
12        if (num == null || index < 0){
13            return 0;
14        }
15        if (index == 0){
16            return num[index];
17        }
18        return Math.max(maxMoney(num, index-1), num[index]+maxMoney(num, index-2));
19    }
20    
21    static int maxMoney2(int[] num){
22        //健壮性
23        int length = num.length;
24        if (num == null || length == 0){
25            return 0;
26        }
27        if (length == 1){
28            return num[length-1];
29        }
30
31        //dp数组, 存放以及计算的值, 优化计算
32        int[] dp = new int[num.length];
33        dp[0] = num[0];
34        dp[1] = Math.max(num[0], num[1]);
35        for (int i = 2; i <length; i++) {
36            dp[i] = Math.max(dp[i-1], dp[i-2]+num[i]);
37        }
38
39        return dp[length-1];
40    }
41    
42    //优化空间复杂度, 只放两个位置.
43    static int maxMoney3(int[] num){
44        //健壮性
45        int length = num.length;
46        if (num == null || length == 0){
47            return 0;
48        }
49        if (length == 1){
50            return num[length-1];
51        }
52
53        //只需要两个变量, 优化空间复杂度从O(n)到O(1)
54        int first = num[0];
55        int second = Math.max(num[0], num[1]);
56        for (int i = 2; i <length; i++) {
57            int temp = second;
58            second = Math.max(second, first+num[i]);
59            first = temp;
60        }
61
62        return second;
63    }
64}
65

首尾相连

街道房间是圆形的. 第一个和最后一个也算是相邻的.

由于第一个和最后一个是互斥的, 于是分解为两个子问题: 第一个房子到倒数第二个房子的最优解, 与第二个房子到最后一个房子的最优解. 分别求出来比较大小.

 1public static void main(String[] args) {
 2        int[] num = new int[]{100, 2, 1, 100};
 3        System.out.println(Math.max(
 4                maxMoney4(num, 0, num.length-2),
 5                maxMoney4(num, 1, num.length-1)
 6        ));
 7    }
 8
 9
10//将下标作为变量, 分别进行最优解运算.
11    static int maxMoney4(int[] num, int start, int end){
12        //健壮性
13        int length = num.length;
14        if (num == null || length == 0){
15            return 0;
16        }
17        if (length == 1){
18            return num[length-1];
19        }
20
21        //只需要两个变量, 优化空间复杂度从O(n)到O(1)
22        int first = num[start];
23        int second = Math.max(num[start], num[start+1]);
24        for (int i = start+2; i <= end; i++) {
25            int temp = second;
26            second = Math.max(second, first+num[i]);
27            first = temp;
28        }
29
30        return second;
31    }

二叉树

父子关系就是相邻的情况.

 1public static void main(String[] args) {
 2        TreeNode node5 = new TreeNode(1, null, null);
 3        TreeNode node4 = new TreeNode(3, null, null);
 4        TreeNode node3 = new TreeNode(3, null, node5);
 5        TreeNode node2 = new TreeNode(2, null, node4);
 6        TreeNode node1 = new TreeNode(3, node2, node3);
 7        //传入根节点
 8        int[] dfs = dfs(node1);
 9        System.out.println(Math.max(dfs[0], dfs[1]));
10    }
11
12
13//深度优先算法
14    public static int[] dfs(TreeNode node){
15        //int[]两个值, 一是选了这个节点select的最优解,第二个是没选这个节点not select的最优解
16        if (node == null){
17            //如果是null节点, 选与不选结果都是1.
18            return new int[]{0,0};
19        }
20        int[] l = dfs(node.left);
21        int[] r = dfs(node.right);
22        //选这个节点意味着不能选下面的节点
23        int select = node.val + l[1] + r[1];
24        //不选这个节点意味着选子节点, 选子节点最大的情况.
25        int notSelect = Math.max(l[0], l[1]) + Math.max(r[0], r[1]);
26        return new int[]{select, notSelect};
27    }

反转链表

1.迭代

用变量保存当前节点和下一个节点的信息, 以此赋值.

 1public class ReverseList {
 2
 3    public static void main(String[] args) {
 4        ListNode node5 = new ListNode(5, null);
 5        ListNode node4 = new ListNode(4, node5);
 6        ListNode node3 = new ListNode(3, node4);
 7        ListNode node2 = new ListNode(2, node3);
 8        ListNode node1 = new ListNode(1, node2);
 9        ListNode iterate = iterate(node1);
10    }
11
12    static class ListNode{
13        int val;
14        ListNode next;
15
16        public ListNode(int val, ListNode next){
17            this.val = val;
18            this.next = next;
19        }
20    }
21
22    public static ListNode iterate(ListNode head){
23        //保存前一个节点
24        ListNode pre = null;
25        //保存当前节点
26        ListNode curr = head;
27        ListNode next;
28        while (curr != null){
29            //先保存下一个节点的信息, 避免被覆盖
30            next = curr.next;
31            //在pre还未指向新的pre之前给自己赋值
32            curr.next = pre;
33            pre = curr;
34            curr = next;
35        }
36        return pre;
37    }
38
39
40}
41

2.递归

以相似的方式重复, 类似于树结构, 从最里面开始遍历.

 1public static ListNode recursion(ListNode head){
 2        if (head == null || head.next == null){
 3            return head;
 4        }
 5        //从最后往前修改
 6        ListNode new_head = recursion(head.next);
 7        head.next.next = head; // 后一个指向前一个
 8        head.next = null; //断原来的链
 9        return new_head;
10    }

素数个数统计

1.暴力算法

对每个数字x继续筛选, 看x是否会被小于根号x的数字整除. 可以用i * i < x 表示根号.

 1public class PrimeSearch {
 2
 3
 4    public static int bf(int x){
 5        int count = 0;
 6        for (int i = 2; i <= x; i++) {
 7            count += isPrime(i) ? 1 : 0;
 8        }
 9        return count;
10    }
11
12    private static boolean isPrime(int i) {
13        for (int j = 2; j * j <= i; j++) {
14            if (i % j == 0){
15                return false;
16            }
17        }
18        return true;
19    }
20}
21

2.埃氏筛选

埃氏筛选: 找到一个质数, 立刻将这个质数所有的倍数都淘汰为合数.

 1    public static int eratosthenes(int n){
 2        int count = 0;
 3        //由于数组下标的因素, 设置为n+1
 4        Boolean[] isPrime = new Boolean[n+1]; //初始化为false
 5        Arrays.fill(isPrime, true); //所有默认为true
 6        for (int i = 2; i <= n; i++) {
 7            if (isPrime[i]){
 8                count++;
 9                //排除所有这个质数的倍数的合数.
10                for (int j = i*i; j <= n; j+=i) {
11                    isPrime[j] = false;
12                }
13            }
14        }
15        return count;
16    }

删除排序数组中的重复项

一个有序数组nums, 原地删除重复出现的元素, 使每个元素只出现一次, 返回删除后数组的新长度

不能使用额外的数组空间, 必须在原地修改数组并在使用O(1)额外空间的条件下完成.

输入: [0,1,2,2,3,3,4]

输出: 5

Java中没有数组元素删除操作, 删除了只能置为null. 或者只能新建数组拷贝.

双指针算法: i(慢指针)和j(快指针)依次指向第一个和第二个, 如果他们对应元素不相等, 则都+1; 如果对应元素相等, 那么j+1; 如果是相等之后出现了不相等, 那么这时将j所在位置的元素赋值给i+1所在位置的元素(nums[i+1]=nums[j]); 如果j到了最后一个, 则返回i.

 1public class SortedArrayDuplicates {
 2
 3    public static void main(String[] args) {
 4        System.out.println(
 5                removeDuplicates(new int[]{0,1,2,2,2,3,3,4})
 6        );
 7    }
 8
 9    public static int removeDuplicates(int[] nums){
10        if (nums.length == 0){
11            return 0;
12        }
13
14        int i = 0;
15        for (int j = 1; j < nums.length; j++) {
16            //当不相等时, 如果是挨着的, 那么nums[i] = nums[j];无影响
17            //如果不是挨着的, 那么会将重复的元素赋值为下一个不重复的元素
18            if (nums[i] != nums[j]){
19                i++;
20                nums[i] = nums[j];
21            }
22        }
23        
24        return i + 1;
25    }
26}
27

寻找数组的中心下标

给定一个整数数组nums, 返回数组"中心下标"的方法, 不存在返回-1, 有多个则返回最靠近左边的那个.

中心下标是数组的一个下标, 其左侧的所有元素相加的和等于右侧所有元素相加的和. 中心下标可能出现在数组的两端.

这道题的关键是理解题意, 左边等于右边, 这是不包括当前位置的值的. 于是思路有

轮到下标为i元素时, 判断0+1+..+i-1+ i 是否等于 sum - 0 - 1 - (i-1). 双方都加一个当前元素等于没有加.

 1public static int pivotIndex(int[] nums){
 2        int sumMinusPrev = Arrays.stream(nums).sum();
 3        int leftPlusCurr = 0;
 4        for (int i = 0; i < nums.length; i++) {
 5            leftPlusCurr += nums[i];
 6            if (leftPlusCurr == sumMinusPrev){
 7                return i;
 8            }
 9            sumMinusPrev -= nums[i];
10        }
11        return -1;
12    }

既然左边右边是相等的, 那么2*(0+1+2+…+i-1) + i = sum总和.

 1public static int pivotIndex2(int[] nums){
 2        int sum = Arrays.stream(nums).sum();
 3        int ima = 0;
 4        for (int i = 0; i < nums.length; i++){
 5            if (ima * 2 + nums[i] == sum){
 6                return i;
 7            }
 8            ima += nums[i];
 9        }
10        return -1;
11    }

验证:

1public static void main(String[] args) {
2        System.out.println(pivotIndex(new int[]{1,7,3,6,5,6}));
3        System.out.println(pivotIndex2(new int[]{1,7,3,6,5,6}));
4    }

X的平方根

不使用sqrt函数, 得到x的平方根的整数部分.

二分法

寻找i * i < x 但 (i+1)*(i+1) > x的值, 使用二分法缩减寻找次数.

 1public static int binarySearch(int x){
 2        int index = -1;
 3        int lP = 0, rP = x;
 4        while (lP <= rP){
 5            //计算新的左右指针的中间值
 6            int mid = (lP + rP) / 2;
 7            if (mid * mid <= x){
 8                lP = mid + 1;
 9                //取小值
10                index = mid;
11            }else {
12                rP = mid - 1;
13            }
14
15        }
16        return index;
17    }

牛顿迭代

原理: x/n 与 n的均值比他们原来更趋近于根号x.

原本的牛顿迭代是迭代选取的点对应切线与x轴交点的值(x1 = x0 - f(x0)/df(x0)),

这里相当于是求x^2-x0=0方程的根, 化简之后就是(i + x/i)/2, 和牛顿迭代一致.

 1public static int newton(int x){
 2        //第一个参数值无所谓, 越接近根号x, 则迭代次数越少.
 3        return (int)sqrt(x, x);
 4    }
 5
 6    public static double sqrt(double i, int x){
 7        double res = (i + x/i)/2;
 8        if (res == i){
 9            return res;
10        }else {
11            sqrt(res, x);
12        }
13    }

数组中三个数的最大乘积

整形数组nums, 在数组中找出由三个数字组成的最大乘积, 并输出.

当数组全为整数时, 最大乘积为前三个最大的数的乘积;

当数组有一个负数时, 最大乘积为前三个最大的数的乘积;

当数组由两个及以上的负数时, 最大乘积为前三个最大的数的乘积和最大的数与两个最小的数的乘积之大者.

先排序后计算

算法复杂度取决于排序算法.

1public static int sortAndCalc(int[] nums){
2        int length = nums.length;
3        Arrays.sort(nums);
4        return Math.max(
5                nums[0]*nums[1]*nums[length-1],
6                nums[length-1]*nums[length-2]*nums[length-3]
7        );
8    }

线性扫描: 只找出前三最大和前二最小

 1public static int getMax3AndMin2(int[] nums){
 2        int max1 = Integer.MIN_VALUE, max2 = Integer.MIN_VALUE, max3 = Integer.MIN_VALUE;
 3        int min1 = Integer.MAX_VALUE, min2 = Integer.MAX_VALUE;
 4        for (int num : nums){
 5            if (num > max1){
 6                max3 = max2;
 7                max2 = max1;
 8                max1 = num;
 9            }else if (num > max2){
10                max3 = max2;
11                max2 = num;
12            }else if (num > max3){
13                max3 = num;
14            }
15
16            if (num < min1){
17                min2 = min1;
18                min1 = num;
19            }else if (num < min2){
20                min2 = num;
21            }
22        }
23
24        return Math.max(
25                max1*max2*max3,
26                max1*min1*min2
27        );
28    }

两数之和–无序数组

给定整数数组nums, 从中寻找两个数满足他们之和为给定目标target.

不可重复使用元素, 返回两数的下标值, 以数组形式返回.

可以使用暴力算法.

或者利用map记录扫描过的数及下标. 这样空间复杂度会稍高.

 1import java.util.Arrays;
 2import java.util.HashMap;
 3import java.util.Map;
 4
 5public class TwoNumberForSum {
 6
 7    public static void main(String[] args) {
 8        System.out.println(
 9                Arrays.toString(solution(new int[]{1, 2, 3, 4, 5, 6}, 10))
10        );
11    }
12
13
14    public static int[] solution(int[] nums, int target){
15        Map<Integer, Integer> map = new HashMap<>();
16        for (int i = 0; i < nums.length; i++) {
17            if (map.containsKey(target - nums[i])){
18                return new int[]{map.get(target - nums[i]), i};
19            }
20            map.put(nums[i], i);
21        }
22        return new int[0];
23    }
24}
25

两数之和–有序数组

二分查找

遍历左边的界限, 在界限之中应用二分查找target-nums[i]的数.

 1public static int[] twoSearch(int[] nums, int target){
 2        for (int i = 0; i < nums.length; i++) {
 3            int low = nums[i], high = nums.length - 1;
 4            while (low <= high){
 5                int mid = (low + high) / 2;
 6                if (nums[mid] == target - nums[i]){
 7                    return new int[]{i, mid};
 8                }else if (nums[mid] > target - nums[i]){
 9                    high = mid - 1;
10                }else {
11                    low = mid + 1;
12                }
13            }
14        }
15        return new int[0];
16    }

双指针

前提是有序.

 1public static int[] twoPointer(int[] nums, int target){
 2        int low = 0, high = nums.length - 1;
 3        while (low < high){
 4            int sum = nums[low] + nums[high];
 5            if (sum == target){
 6                return new int[]{low, high};
 7            }else if (sum > target){
 8                high--;
 9            }else {
10                low++;
11            }
12        }
13        return new int[0];
14    }

计算斐波那契数列

0, 1, 1, 2, 3, 5, 8, …. 后一项等于前面两项的和.

暴力递归

直接递归, 这样有些项存在严重的重复计算.

1public static int BFRecursion(int num){
2        if (num == 0) return 0;
3        if (num == 1) return 1;
4        return BFRecursion(num - 1) + BFRecursion(num - 2);
5    }

去重递归

用空间保存计算过的项. 时间O(n) 空间O(n)

 1public static int SavedRecursion(int num){
 2        //由于第一个是0, 所以需要多一个空间.
 3        int[] saveArr = new int[num + 1];
 4        return Recursion(saveArr, num);
 5    }
 6
 7    private static int Recursion(int[] saveArr, int num) {
 8        if (num == 0) return 0;
 9        if (num == 1) return 1;
10        //如果之前这个位置已经被运算, 直接返回.
11        if (saveArr[num] != 0) return saveArr[num];
12        saveArr[num] = Recursion(saveArr, num - 1) + Recursion(saveArr, num - 2);
13        return saveArr[num];
14    }

双指针迭代

只需要两个位置保存, 节省了空间至O(1)

 1public static int TwoPointer(int num){
 2        if (num == 0) return 0;
 3        if (num == 1) return 1;
 4        int first = 1, second = 0;
 5        for (int i = 2; i <= num; i++) {
 6            int temp = first;
 7            first = first + second;
 8            second = temp;
 9        }
10        return first;
11    }

排列硬币

n枚硬币, 将他们排列为阶梯形状, 第k行有k枚硬币.

给定一个数字n, 找出可形成完整阶梯行的总行数. 就是可以剩, 不需要全部用完.

暴力迭代

啥也不管, 一行一行地排

1public static int arrangeCoinBF(int n){
2        for (int i = 1; i < n; i++) {
3            n -= i;
4            if (n < i + 1){
5                return i;
6            }
7        }
8        return -1;
9    }

二分查找

行数必定在0到n之间, 查找这之中满足求和=n的值, 找不到就返回最大的行使求和<n.

 1public static int arrangeCoinSearch(int n){
 2        int low = 0, high = n - 1;
 3        while (low < high){
 4            int mid = (low + high) / 2;
 5            int predict = ((mid + 1) * mid) / 2;
 6            if (n == predict){
 7                return mid;
 8            }else if (n < predict){
 9                high = mid - 1;
10            }else {
11                low = mid + 1;
12            }
13        }
14        return low;
15    }

牛顿迭代

给定总数n求行数x, 由于 (x^2 + x) /2= n, 想求对应的x, 实际上是函数f(x) = (x^2 + x) /2 - n的根, 于是可以采用牛顿迭代, 每次迭代x1 = x0 - f(x0)/df(x0) = (x0^2 + 2n)/(2x0+1), 如果从n开始迭代, 则第一次为

1public static double newtonRecursion(int n, int res){
2        res = (res * res + 2 * n) / (res * 2 + 1);
3        if (res * res + res == 2 * n){
4            return res;
5        }else {
6            return newtonRecursion(n, res);
7        }
8    }

环形链表

给定额链表, 判断链表中是否有环(如果链表有某个节点可以通过连续跟踪next指针再次到该节点, 就存在环). 存在环返回true, 否则返回false.

内部类:

 1//内部类
 2    static class ListNode{
 3        int val;
 4        ListNode next;
 5
 6        public ListNode(int val, ListNode next){
 7            this.val = val;
 8            this.next = next;
 9        }
10    }
11
12    public static void main(String[] args) {
13        ListNode node5 = new ListNode(5, null);
14        ListNode node4 = new ListNode(4, node5);
15        ListNode node3 = new ListNode(3, node4);
16        ListNode node2 = new ListNode(2, node3);
17        ListNode node1 = new ListNode(1, node2);
18        //node5.next = node3;
19
20        System.out.println(isCycle(node1));
21        System.out.println(isCycleTwoPointer(node1));
22    }

普通循环

时间O(n), 空间O(n)

 1public static Boolean isCycle(ListNode head){
 2        HashSet<ListNode> set = new HashSet<>();
 3        while (head != null){
 4            if (!set.add(head)){
 5                return true;
 6            }
 7            head = head.next;
 8        }
 9        return false;
10    }

双指针

如果快指针和慢指针可以重叠, 说明存在环; 如果快指针到达了null, 说明没有环.

时间O(n), 空间O(1)

 1public static Boolean isCycleTwoPointer(ListNode head){
 2        if (head == null || head.next == null) return false;
 3        ListNode slow = head;
 4        ListNode fast = head.next;
 5        while (fast.next != null && fast.next.next != null){
 6            if (slow == fast) return true;
 7            slow = slow.next;
 8            fast = fast.next.next;
 9        }
10        return false;
11    }

合并两个有序数组

两个有序整数数组nums1和nums2, 将nums2合并到nums1中, 使nums1成为一个有序数组. nums1和nums2元素个数分别为m和n, 假设nums1的空间大小等于m+n.

合并后排序

取决于排序的时间复杂度O(N*logN), 不消化额外空间

1//m为nums1实际元素个数, n为nums2实际元素个数
2    public static int[] mergeAndSort(int[] nums1, int m, int[] nums2, int n){
3        //将数组2拷贝至数组1的后面.
4        System.arraycopy(nums2, 0, nums1, m, n);
5        //排序, 复杂度取决于排序的复杂度, 为N*logN
6        Arrays.sort(nums1);
7        return nums1;
8    }

双指针

需要消耗O(n)的空间

 1public static int[] compareAndInsert(int[] nums1, int m, int[] nums2, int n){
 2        //要求返回nums1, 所以我们需要处理一下.
 3        int[] num1Copy = new int[m];
 4        System.arraycopy(nums1, 0, num1Copy, 0, m);
 5        int pointerNum1 = 0, pointerNum2 = 0;
 6        int i = 0;
 7//        int[] res = new int[m+n];
 8
 9        while (pointerNum1 < m && pointerNum2 < n){
10            //被选中的才会++, 且是先用后++.
11            nums1[i++] = num1Copy[pointerNum1] < nums2[pointerNum2] ? num1Copy[pointerNum1++] : nums2[pointerNum2++];
12//            if (nums1[pointerNum1] > nums2[pointerNum2]){
13//                res[i] = nums2[pointerNum2];
14//                pointerNum2++;
15//            }else {
16//                res[i] = nums1[pointerNum1];
17//                pointerNum1++;
18//            }
19//            i++;
20        }
21        if (pointerNum2 < n){
22            System.arraycopy(nums2, pointerNum2, nums1, pointerNum1 + pointerNum2, m + n - pointerNum2 -pointerNum1);
23        }
24        if (pointerNum1 < m){
25            System.arraycopy(num1Copy, pointerNum1, nums1, pointerNum1 + pointerNum2, m + n - pointerNum2 -pointerNum1);
26        }
27        return nums1;
28    }

倒着排

 1 public static int[] reverseMerge(int[] nums1, int m, int[] nums2, int n) {
 2        int p1 = m - 1, p2 = n-1;
 3        int i = m+n-1;
 4
 5        while (p1 >= 0 && p2 >= 0) {
 6            nums1[i--] = nums1[p1] > nums2[p2] ? nums1[p1--] : nums2[p2--];
 7        }
 8        //有两种情况, 1是nums2下标先走完至-1, 这时无序任何操作
 9        //2是nums1下标先走完至-1, 这是nums2还有额外的元素需要复制
10        System.arraycopy(nums2, 0, nums1, 0, p2 + 1);
11        return nums1;
12    }

子数组最大平均数

给一个整数数组, 找出平均数最大且长度为k的下标连续的子数组, 并输出该最大平均数.

输入: [1,12,-5,-6,50,3], k=4

输出: 12.75

最大平均数 (12-5-6+50)/4=12.75

滑动窗口

是双指针的特例:

 1public static double twoPointer(int[] nums, int k){
 2        int pl = 0, pr = k-1;
 3        int maxSum = 0;
 4        for (int i = pl; i <= pr; i++) {
 5            maxSum += nums[i];
 6        }
 7
 8        while (pr < nums.length - 1){
 9            int tempSum = maxSum -nums[pl] + nums[pr+1];
10            if (tempSum > maxSum) maxSum = tempSum;
11            pl++;
12            pr++;
13        }
14
15        return 1.0 * maxSum/k;
16    }

由于长度固定, 故只需要一个指针:

 1public static double slideWindow(int[] nums, int k){
 2        int sum = 0;
 3        for (int i = 0; i < k; i++) {
 4            sum += nums[i];
 5        }
 6        int max = sum;
 7
 8        for (int i = k; i < nums.length; i++) {
 9            sum = sum - nums[i-k] + nums[i];
10            max = Math.max(sum, max);
11        }
12
13        return 1.0 * max/4;
14    }

二叉树的最小深度

最小深度是从根节点到最近叶子节点的最短路径上的节点数量.

深度优先

先找到叶子节点, 然后从叶子节点往上找, 计算每个节点的最小深度(取左右叶子节点较小的那个+1.

空间复杂度O(logN) 取决于树的深度, 时间复杂度O(N)

 1	public static int minDepth(TreeNode root) {
 2        //空节点
 3        if (root == null) return 0;
 4        //叶子节点
 5        if (root.left == null && root.right == null) return 1;
 6
 7        int min = Integer.MAX_VALUE;
 8        //寻找左右子节点中最小的深度
 9        if (root.left != null) min = Math.min(min, minDepth(root.left));
10        if (root.right != null) min = Math.min(min, minDepth(root.right));
11
12        //最后加上本节点的1返回.
13        return min + 1;
14    }

广度优先

一层一层遍历, 遍历到的第一个叶子节点就是最小深度.

空间复杂度取决于队列O(N), 时间复杂度O(N)

 1public static int minWidth(TreeNode root){
 2        if (root == null) return 0;
 3
 4        //由于队列的性质, 它是广度遍历. 遍历完同一层才会遍历下一层
 5        Queue<TreeNode> queue = new LinkedList<TreeNode>();
 6        root.setDeep(1);
 7    	//入队
 8        queue.offer(root);
 9
10        while (!queue.isEmpty()){
11            //出队
12            TreeNode node = queue.poll();
13
14            //遍历到根节点直接返回
15            if (node.left == null && node.right == null){
16                return node.deep;
17            }
18
19            if (node.left != null) {
20                node.left.setDeep(node.getDeep() + 1);
21                queue.offer(node.left);
22            }
23            if (node.right != null){
24                node.right.setDeep(node.getDeep() + 1);
25                queue.offer(node.right);
26            }
27        }
28        
29        //非正常退出
30        return -1;
31    }

最长连续递增序列

给定一个未排序的整数数组, 找到最长且连续递增的子序列, 并返回该序列的长度.

方式一: 记录当前序列的开始位置, 如果后面的数字小于这个序列最后一个数, 则更新开始下标.

方式二: 直接记录最大序列的长度和当前序列的长度.

 1public class MaxSeq {
 2
 3    public static void main(String[] args) {
 4        System.out.println(findLength(new int[]{1,2,3,2,3,4,3,4,5,6,7}));
 5    }
 6
 7    public static int findLength(int[] nums){
 8        int start = 0;
 9        int max = 0;
10        for (int i = 1; i < nums.length; i++) {
11            if (nums[i] < nums[i-1]) start = i;
12            max = Math.max(max, i - start + 1);
13        }
14        return max;
15    }
16}
17

柠檬水找零

每杯柠檬水5美元, 顾客排队买, 顾客只会付5, 10, 20美元, 必须给顾客正确找零. 一开始手里面没有任何零钱, 如果能正确找零返回true, 否则返回false.

分析: 对于顾客付的5美元, 直接收下; 对于顾客付的10美元, 只能找5美元; 对于20美元, 可以三个5, 也可以10+5, 但是为了局部最优, 最好10+5. 因为这里5是万能的, 尽量减少使用.

 1public class LemonWater {
 2
 3    public static void main(String[] args) {
 4        System.out.println(isCanGiveChange(new int[]{5,5,5,20}));
 5
 6    }
 7
 8    public static boolean isCanGiveChange(int[] nums){
 9        //5和10的票子数量
10        int fiveNum = 0, tenNum = 0;
11        for (int num: nums) {
12            switch (num){
13                case 5:
14                    fiveNum++;
15                    break;
16                case 10:
17                    if (fiveNum > 0){
18                        fiveNum--;
19                        tenNum++;
20                    }else
21                        return false;
22                    break;
23                case 20:
24                    if (fiveNum > 0 && tenNum > 0){
25                        fiveNum--;
26                        tenNum--;
27                    }else if (fiveNum >= 3){
28                        fiveNum -= 3;
29                    }else
30                        return false;
31            }
32        }
33
34        return true;
35    }
36}
37

三角形的最大周长

给一个正数数组arr, 返回由其3个数组成的, 面积不为0的三角形的周长可能的最大值.

直接找最大和的三个数, 看看是否能形成三角形, 不行就减少最大数继续. 因为既然最大的三个数不行, 那么前两最大的数和任何一个数都不行了, 所以只能往下找.

 1import java.util.Arrays;
 2
 3public class Triangle {
 4
 5    public static void main(String[] args) {
 6        System.out.println(maxPerimeter(new int[]{3,6,3,2}));
 7    }
 8
 9    public static int maxPerimeter(int[] nums){
10        Arrays.sort(nums);
11        for (int i = nums.length - 1; i >= 2 ; i--) {
12            if (nums[i-1] + nums[i-2] > nums[i]){
13                return nums[i] + nums[i-1] + nums[i-2];
14            }
15        }
16        return 0;
17    }
18}
19

二叉树遍历

前序

递归实现

1//前序:根左右
2    public static void preorder(TreeNode root){
3        if (root == null) return;
4
5        System.out.println(root.val);
6        preorder(root.left);
7        preorder(root.right);
8    }

中序

递归实现

 1 //中序
 2    public static void midorder(TreeNode root){
 3        if (root == null) return;
 4
 5        if (root.left != null){
 6            preorder(root.left);
 7        }
 8
 9        System.out.println(root.val);
10
11        if (root.right != null){
12            preorder(root.right);
13        }
14
15    }

后序

递归实现

 1//后序
 2    public static void postorder(TreeNode root){
 3        if (root == null) return;
 4
 5        if (root.left != null){
 6            preorder(root.left);
 7        }
 8
 9        if (root.right != null){
10            preorder(root.right);
11        }
12
13        System.out.println(root.val);
14    }

层序

递归实现

 1//层序遍历
 2    //这个参数i代表的第几层, 由于树不是完全的, 所以一定之间会有null值
 3    public static void levelorder(TreeNode root, int i, ArrayList list){
 4        if (root == null) return;
 5
 6        int length = list.size();
 7        //为防止数组越界, 这里提前填充至i.
 8        if (length  <= i){
 9            for (int j = 0; j <= i - length; j++) {
10                list.add(length+j, null);
11            }
12        }
13
14        list.set(i, root.val);
15        levelorder(root.left, 2*i, list);
16        levelorder(root.right, 2*i+1, list);
17    }

目录

字符串搜索

BF: 暴力破解

RK算法: hash算法

BM算法

KMP算法

打家劫舍

初始问题

首尾相连

二叉树

反转链表

1.迭代

2.递归

素数个数统计

1.暴力算法

2.埃氏筛选

删除排序数组中的重复项

寻找数组的中心下标

X的平方根

二分法

牛顿迭代

数组中三个数的最大乘积

先排序后计算

线性扫描: 只找出前三最大和前二最小

两数之和–无序数组

两数之和–有序数组

二分查找

双指针

计算斐波那契数列

暴力递归

去重递归

双指针迭代

排列硬币

暴力迭代

二分查找

牛顿迭代

环形链表

普通循环

双指针

合并两个有序数组

合并后排序

双指针

倒着排

子数组最大平均数

滑动窗口

二叉树的最小深度

深度优先

广度优先

最长连续递增序列

柠檬水找零

三角形的最大周长

二叉树遍历

前序

递归实现

中序

递归实现

后序

递归实现

层序

递归实现

相关文章